On the Proximity and Collinearity Coefficients of Planetary Time Series

A Note on the Proximity and Collinearity Coefficients of Planetary Time Series

The correlation coefficient

, taken as a measure of collinearity in time series

, is shown to depend on the ratio of two variances and then invariant on the inclination

of the regression line relative to the Cartesian co-ordinated axes. Also invariant with the inclination

is the mean distance

of the discrete data points to the regression straight line. This is taken as a measure, a coefficient of proximity. Analysis of these coefficients (

and

) and their invariance with rotation of the co-ordinate system, from synthetic series, allowed the definition of a variable

that is also invariant and may be taken as a constant, which characterises each of the constrained planetary series and, in consequence, the F distribution of the entire set of PSMSL sea level series. Analyses of statistical variables such as collinearity

and trends

, show that they are mutually independent, but the whole set of values calculated from PSMSL series, seems world widely distributed as dependent variables, due to limits geo-physically imposed on them as planetary series. The study of this induced dependence may help to unveil the characteristics of the planetary constraints.

The PSMSL (Permanent Service of the Mean Sea Level) of IAPSO ( International Association for the Physical Sciences) series of sea level data, is a unique world wide almost evenly distributed set of series, measuring the sea level, as well as the level of Earth´s crust, as they are world wide series of relative sea level and not series of absolute sea level values.

As such, this communication explores the relationships between parameters of time series data shown in Fig 1, such as trends

, angles

, values of

tan(

), distances

of data points to the regression line, and correlations

, with the aim of better understanding the geophysical information in a set of PSMSL sea level series (Spencer & Woodworth, 1993), taken here as a planetary data set.

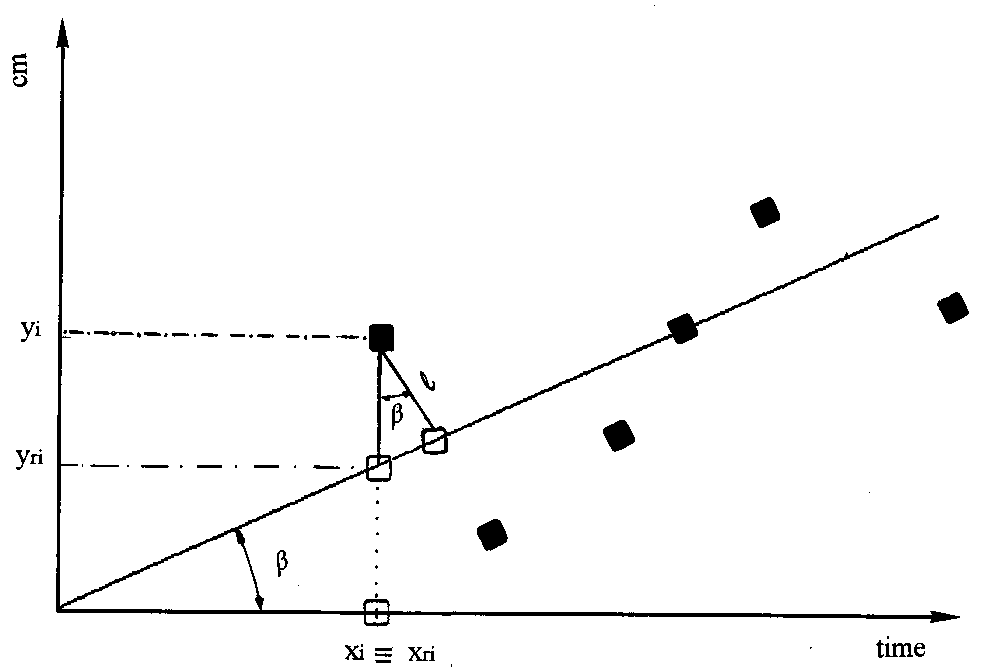
Fig. 1 - The regression line and its generating points (black spots). l is the distance of the point X(x_i, y_i), i=1,...,n, to the straight line. Its projection on the straight line X(x_ri, y_ri) is represented by a white square is the inclination of the straight line relative to the x axis.

The plot of annual values of these series have trends

, that appear to be physically constrained by the planet Earth relative to its surface to maximum values, say ,within

60 mm/year, as the planet, in the scale of years, does not change its volume or shape abruptly.

Not submitted to these constraints 5,500 noisy ordinary time series, with 5 to 60 equivalent years lengths , were computer built, forced to acquire

values within about

40, and from them, the distances

, (the proximity of the data points to the straight line) and also the correlation coefficients

, (the collinearity of the data points along the straight line) were calculated .

Similarly, the proximity coefficients

, the collinearity coefficients

, and the corresponding trends

from real mean annual values of 837 PSMSL planetary series, with different lengths, greater than 5years, were calculated .

Expressions usually used the data points distance

in terms of

and the Cartesian axes . Also expressions of

in terms of the covariance (COV) of the points on the regression line y

(

) =

, and the actual data points y(t

), divided by the standard deviation of y

(

) and also the collinearity

coefficient expressed in terms of the same covariance (COV) divided by the product of the standard deviations of y

(

) and y(t

), i = 1,2,3,.......,n. (n = number of points of each series). Their ratio expressed in terms of two variances is shown to be independent of the trends

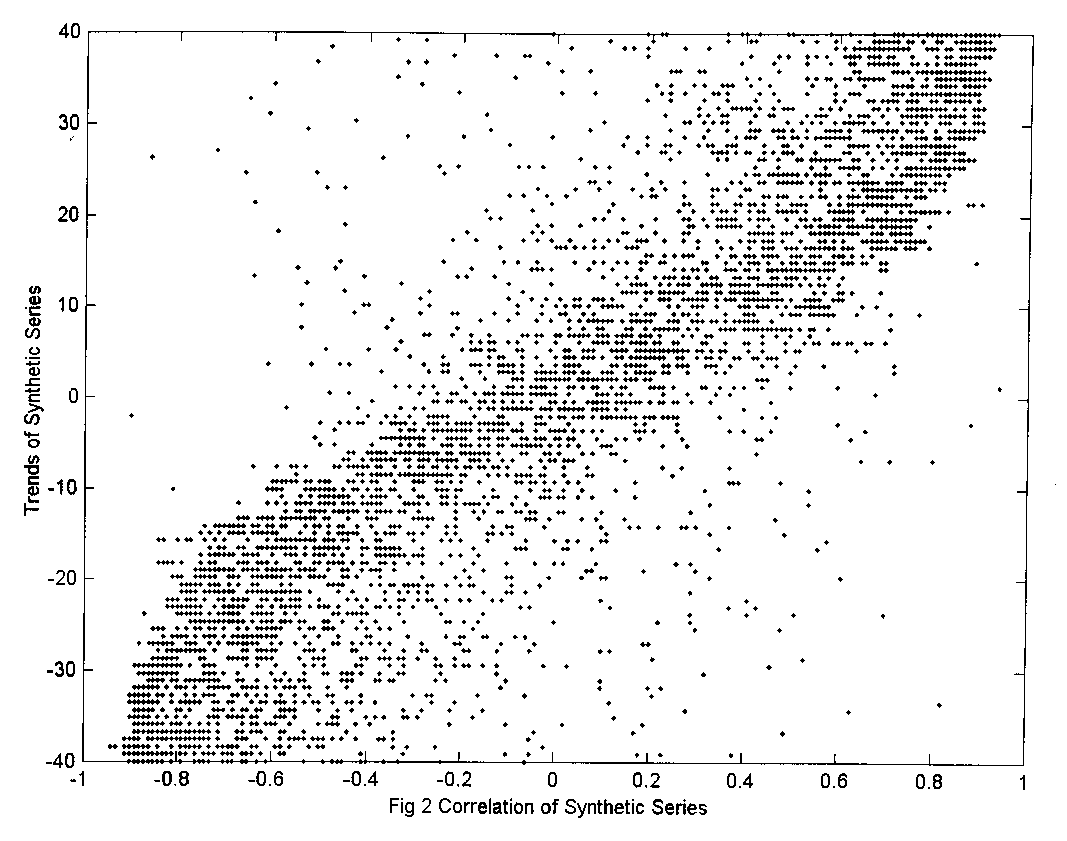
Results show that, while for the synthetic series collinearity

is independent of the values of the

, Fig 2, the whole set of real constrained series have collinearity

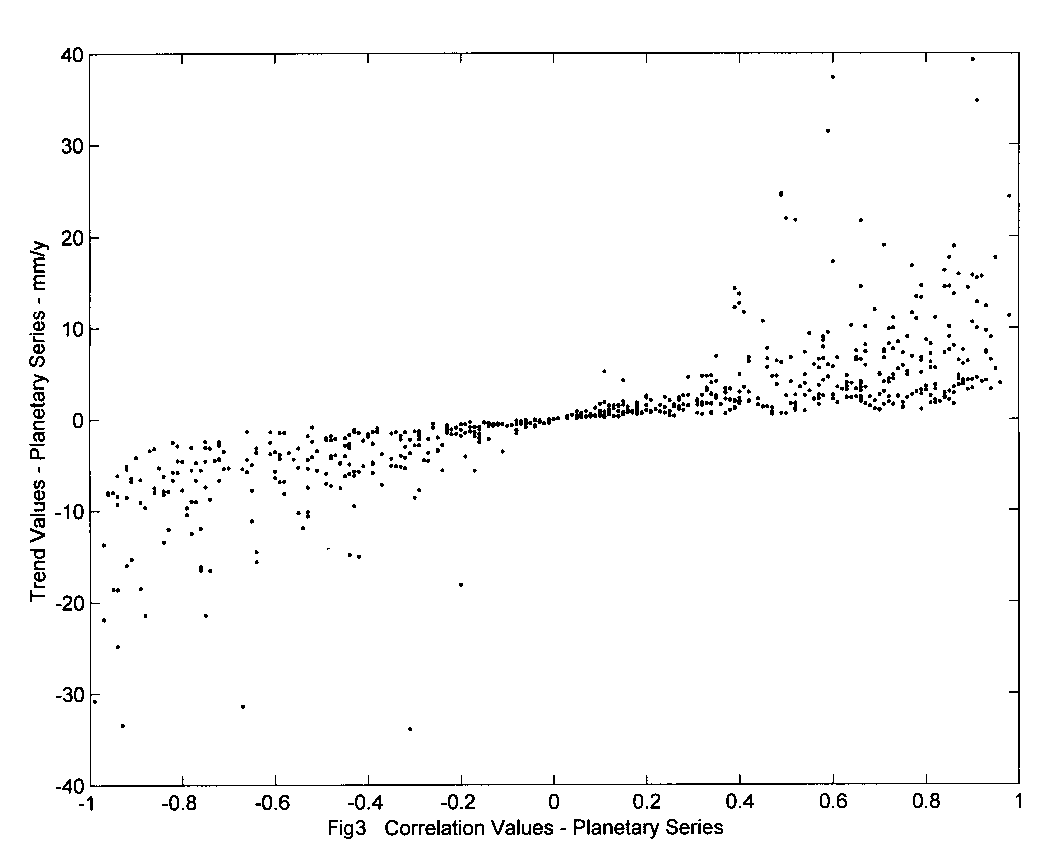
values that seem to be dependent of the trend

. In consequence the plot of

for planetary series Fig 3, revealed a curve, that should have not followed either

, as in fact they seem to be doing, and this is interpreted as the unveiling of an Earth’s free response, that is in printed on the entire set of planetary constrained series used.

, the proximity coefficients and

, the collinearity coefficients for a given planetary series, are both independent of the trend

, (as also are the

and

values of the synthetic series relative to

), a function

is defined, that is independent of

, which is, possibly, also another characteristic of mass and gravity constrained planetary series.

The distribution curve of

may have, with the glaciations, an evolving timely constant shape, that is a characteristic of the Planet Earth, where in Fig 11, few identified ports of Africa, Europe and the Americas, should hold , in the present days, relatively permanent positions.

Given a circular line, (a circumference), with a set of points that normally distributed, surrounds it, a sort of correlation, which measures how close or disperse are the points from the circular line, may be formulated. The correlation, with this meaning (correlation as a measure of proximity of the cloud of points to the circumference), is clearly invariant with the rotation of the system of Cartesian co-ordinates fixed, for example, in its centre, as the mean distance of all points to the circumference is a geometric property of the space time and it will not vary with a variable orientation of the co-ordinate axis.

By rectification , the circumference, (or any other closed curve) and the accompanying set of points can be transformed into a segment of straight line, a one dimensional figure, with its bi-dimensional accompanying set of points,( Fig 1). Assuming a one dimensional normal distribution of the point's distances to the line, the normalised standard deviation of the distances of the set can be devised. It can be realised in this circumstance that the standard deviation of the distances of the points to the central line will be great ( when the points are totally apart from the line) and zero (when all points lye on the line) and may be taken as a measure of the correlation of the surrounding set of points with the straight line.

In fact, from Fig 1 it can be seen that from the Cartesian co-ordinates of a point y

, belonging to the cloud of points and from the inclination

of its straight line, it is possible to infer the co-ordinates xr

;yr

of its projection on the line, and the distance of length

so that:

As one can see

, as an Euclidean distance, is necessarily invariant with the inclination

and the corresponding co-ordinates of the point x

; y

, as the system of reference rotates in the plane of the Figure. For any variation of

the co-ordinates x

and y

should acquire correspondingly adequate values so that the above expressions satisfy the physical distances

as constants.

However, in Fig 1 the correlation can also be a measure of linear dependence between the set of points that surrounds the line and the ones belonging to it, if they can be taken somehow as a random variable, as in the special case of time series in which x

= t

and can not be taken as a random variable. That makes the above inferences not so clear and here on, because of that , the name of collinearity is chosen as more appropriate to nominate this sort of correlation, i.e., the correlation of values of a random variable y(t

) with those on the straight line y

(

) =

The known concept of correlation is of a measure of linear dependence between two random variables ( Jenkins and Watts, 1978) and, in the limiting case, when the correlation is one, there is an exact linear relationship of the form

where

= tan(

) is the regression coefficient and

is the intercept, i=1,2,3.....n.

When the correlation

is zero there is no linear dependence between the two random variables. In the case for correlation zero,

= tan(

) may assume any value from -

to +

and the inclination

of the line will take any value within

/2.

The question which arises now is if the two ways of interpreting the correlation, as a measure of the proximity

of the cloud to the line, or as a measure of the colinearity

of the points of the cloud, can be both invariant with the rotation of the co-ordinate system, as already does the first interpretation.

To examine that let X and Y be two random variables with values x

and y

and that one wishes to approximate the values of Y by a linear combination of the form: y

. Following the method of minimum squares, the differences of the random variable Y and the above adjusted line is used to form the sum of squared error as:

Symbols with a ^ are sample estimates and from here to the end

tan(

) also represents the regression coefficient; the ^ will be omitted from now on.

By making the derivatives of

relative to

and

equal to zero and equating the resulting expressions for

, one obtains:

By expanding the above expression and by adding and subtracting in the denominator

where

indicates collinearity , when time t

is taken linearly to represent the variable x

= t

As the proximity

and the collinearity

coefficients are to be invariant with the values of the inclination angle

and

, it is convenient to define a variable

that should also be independent of the inclinations

and has the form:

relates the coefficients of proximity

and collinearity

and is a constant for each constrained planetary series, as the sea level series of the PSMSL y(

, that will be used here.

The same can be said about F for a set of synthetic series y1(t

), each series with n = 6 to 60 values and with regression coefficients

forced to vary from – 40 to + 40, which were generated for this study. To each assigned regression coefficient, a random value was synthetically added and also another random value added to the derived y

) value, in order to produce series free of constraints. Values of

and

were calculated for all synthetic and the constrained PSMSL series and the results were compared.

The application of the expressions of previous section, follows the methodology along which one has to correlate the straight line values y

) given by its estimated coefficient of regression

= tan(

) with the data, given by any well behaved function of time y(t

). In order to relate the

and

values one can divide their expressions above, to obtain:

but

has a real value that can, in all cases, be divided by

0, producing a real number

, not always equal to

, and the above value is reduced to:

where mo is a dimensionless constant less or equal to one . In this circumstance the collinearity coefficient

is, for each regression line, independent of the inclination, or rather, the regression coefficient given by

= tan(

) , as sought for . For a given

there will be always a

to make the quotient equal to mo.

The independence of the collinearity coefficient

with

can be seen in Fig 2, where their values for synthetic series are plotted. The distribution of

values around a nearly diffuse figure characterises the plotting of independent values.

The graph of

and trends

of real constrained (by conservation of mass and gravity) series of PSMSL shown in Fig 3 indicates, on the contrary, that although their collinearity and trends are statistically independent, they as a set do show to be planetary dependent variables. Meaning that, as statistical variables they are independent, but the whole set is distributed in Fig 3 as they were dependent, due to what seems to be the limits geo-physically imposed on planetary series.

The gravitacional field and the nearly constant mass of the planet Earth is apparently a constraint that induces the dependence on the estimates of statistical variables, which are, from their definition, statistically independent . The study of this induced dependence may help to unveil the characteristics of the planetary constraints.

A common characteristic of synthetic and planetary series is related to the way synthetic series were generated in the computer, causing the distribution graph of the collinearity values

of the real planetary series of PSMSL, as shown in Fig 4, and distribution graph for the synthetic series Fig 5, to be both nearly uniform. The uniform distribution of correlation values indicates that collinearity values appear in the entire set of series with equal frequency from –1 to + 1 , including the value zero in the synthetic and real series.

A different characteristic is that the distribution trends

is somewhat Gaussian for planetary series, as shown in Fig 6, while the distribution of

for synthetic series is nearly Uniform, forced by the way they were computed, as can be seen in Fig 7. This causes the graph

for the synthetic series, to have a diffuse shape as shown in Fig 2 around a more intense core defined by the imposed variation of

from –40 to +40, while for the planetary series, the equivalent graph has a peculiar configuration, Fig 3. As can be seen, in Fig 3, values of

equal 0 correspond only to trend

values that are equal to 0, while for synthetic series

= 0 corresponds to any value of

as required by independent variables .

Again different characteristics are shown by

graphs. For synthetic series, high values

( - 40 and + 40 ) correspond to small values of (

=140 ) (Fig 8), while the opposite occurs for the planetary series, (with a cuspid like shape), that shows for low values of trends

( near 0) corresponding the greatest proximity value (

=90 mm); in this last case great trend values

(-40 and +40 mm/year) to correspond the smallest distances

, nearly 0.

It is worth noticing that for synthetic series the distances

were calculated from the expression of

= (y

– y

) cos

, given in the Introduction for a given constant difference (y

– y

) = - 60, so that for

varying within – 40 to + 40 , the smallest values of

are at the extremes of

and the highest

values when

= 0. This is shown in Fig 8 and in Fig 12, plots of

values against

and

, respectively, for synthetic series. This does not mean that distance

is not invariant with

. It only stays the way different values of

were calculated.

Proximity coefficients

for planetary series calculated by using the same expression

= (y

– y

) cos

have a different distribution, as can be seen in Fig 13. For collinearity values near to + 1 or –1 the distances

are close to zero, while for collinearity values near zero the values of

are close to 90, as expected from their definition . The smallest distance

corresponds to collinearity values nearly equal to one and for

= 0 the values of

are at their maximum values.

A general characteristic seen in Figs 10 and 11 is that for both, planetary and synthetic series, the distributions of F follow the assertions that the product

vary with

and

and conforms to be F= 0, when

is zero (and

equals one) and turns to be F = zero, when

reaches its greatest values ( and correspondingly

is equal zero).

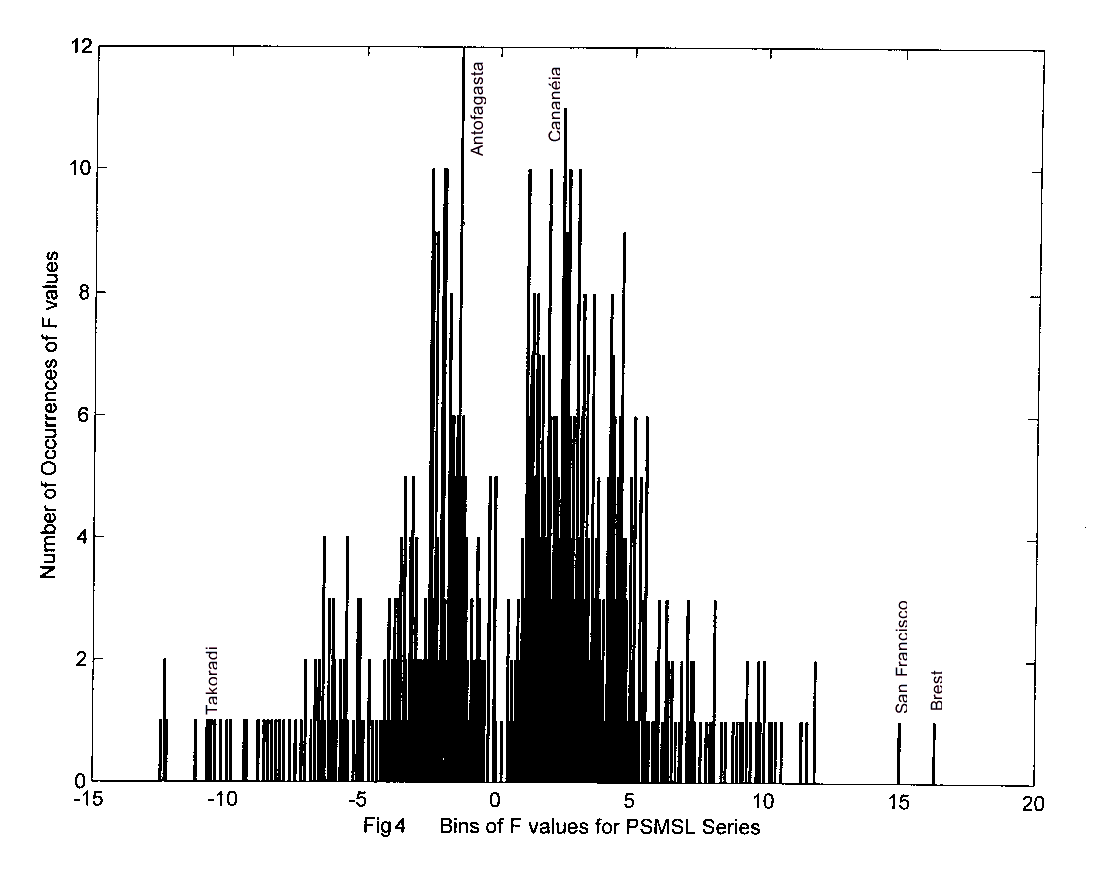
Occupying nearly permanent positions in the F distribution of Planetary PSMSL series, plots of F distribution shows , Fig 11, for ports of San Francisco, F=14.95, for Antofagasta, F= -3.550, for Cananeia, F = 4.565, for Balboa, F = 8.774 and for Brest, F=16.305 . All PSMSL ports can also be identified in the F distribution graph. Further work is under way examining the point.

The correlation coefficient

, taken as a measure of collinearity, and the mean distance

, taken as a measure of proximity of the discrete data points to the regression straight line, in time series, are both invariant on the inclination

of the regression line relative to the Cartesian co-ordinated axes and, in consequence, their product is also independent. It was defined then the function

The invariance of F values with trends

for each series and in consequence its distribution graph, may be useful to examine aspects of the planet Earth, that only arise from the study of world wide evenly distributed planetary time series, as the set of PSMSL data. Collinearity

and trends

of PSMSL indicate that although they are statistically independent, they as a set are planetary dependent variables due to what seems to be the limits geo-physically imposed on planetary series.

We are grateful to Dr Philip Woodworth , Dr Ian Vassie and Robert and Elaine Spencer of POL (Proudman Oceanographic Laboratory), Liverpool, UK, for their continued support and for providing the PSMSL series for this work . Dr Joseph Harari critically revised the manuscript.

Jenkins, G M & Watts, D G , 1968 . Spectral Analysis and its Applications. Holden Day, London..523 p..

Spencer E N & Woodworth P L. 1993. Data Holdings of the Permanent Service for the Mean Sea Level. Bidston . Birkenhead. Merseyside, L437RA, UK. 81p