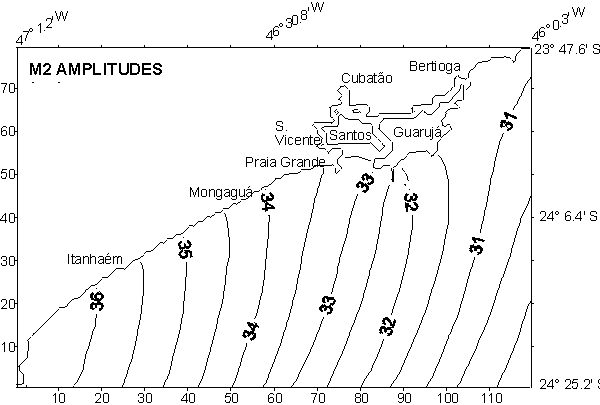
Fig. 1 - M2 amplitudes in Santos.
Ricardo de Camargo1, Joseph Harari2
& Amaury Caruzzo3
1, 3 Institute of Astronomy and Geophysics
2 Institute of Oceanography
University of São Paulo - Brazil
In this study, the Princeton Ocean Model - POM was implemented
for the coastal regions of Santos (Sao Paulo State) and Paranagua (Parana
State). The models were processed for high resolution tidal simulations,
considering a grid spacing of about 1 Km and tidal oscillations at the
boundaries given by the shelf model of Harari & Camargo (1994). Characteristics
of the tidal propagation in the modelled areas were obtained, leading to
operational regional systems of tidal and tidal currents predictions (Harari
& Camargo, 1997, 1998).
The version of POM that was implemented has the following characteristics
(Blumberg & Mellor, 1987; Mellor, 1993): use of the full 3D hydrodynamical
equations, written in flux form, under the hydrostatic and Boussinesq approximations;
vertical solution based on sigma coordinates; second order turbulent clousure
for the vertical diffusion; Smagorinsky parametrization for the horizontal
diffusion; mode splitting; explicit leapfrog method for the numerical integration
in time and the horizontal; and implicit method for the vertical integration
of the equations.
Both models considered horizontal spacing of approximately 1
Km and 11 sigma levels, placed at 0.0 (surface), -0.03125, -0.0625, -0.125,
-0.25, -0.5, -0.75, -0.875, -0.9375, -0.96875 and -1.0 (bottom); the time
steps were 15 s (for the external mode) and 300 (for the internal modes);
the frictional parameters used in the models were the same of Oey, Mellor
& Hires (1985). For the coastal region of Santos, a regular cartesian
grid of 120 x 80 cells was used, with 5527 wet points; for the coastal
area of Paranagua, the regular grid has 90 x 70 cells, 3122 of them being
wet.
Tidal oscillations were specified both at the open boundaries
and the first internal lines and columns of the grid, in order to avoid
the need of current specifications. These boundary conditions had to be
corrected, with supplementary tidal amplifications and delays, after comparing
preliminary model results with tidal analyses of the Ports of Santos and
Paranagua. The final results of the models matched the tidal predictions
of these ports with errors in elevations of less than 5%.
For Santos, the open boundary oscillations considered components
Q1, O1, P1, K1, N2, M2, S2, K2 and M3, which account for more than 90%
of the tidal energy in the area; on the other hand, the Paranagua simulations
required additionally components MN4 and MS4 at the borders, due to their
important contribution to the tidal range in the inner estuarine areas.
The models run with uniform density and no meteorological effects,
for a period of 31 days, starting from zero elevations and currents; the
hydrodynamic equilibrium was reached at the end of approximately 2 days
so that series of 696 hourly results (29 days) were obtained.
The computed time series of surface elevations and currents,
of all wet grid points, were analysed through the Harmonic Method of Tidal
Analysis (Franco, 1988; Franco & Harari, 1987). The analyses results
were used for mapping the elevation cotidal lines and the axes of the surface
tidal current ellipses.
Figures 1 to 4 present the cotidal maps for component M2, the
most energetic among those considered in the models. The common features
of all the principal tidal components are the significant amplitude gradients
and phase delays towards the shallow internal regions; for instance, the
M2 amplitudes ranged from 30 to 40 cm in Santos and from 30 to 50 cm in
Paranagua. In fact, the models allowed very accurate computations of the
tidal propagations in the estuaries, resolving variations of tenth of centimeters
(in amplitude) and few minutes (in phase); as examples, Figures 5 and 6
present the M2 propagation into the internal channels in the region of
Santos; strong tidal currents are associated to this shallow area circulation,
with intensities reaching nearly 50 cm/s, as shown by the M2 tidal ellipses
in Figure 7.

Fig. 1 - M2 amplitudes in Santos.
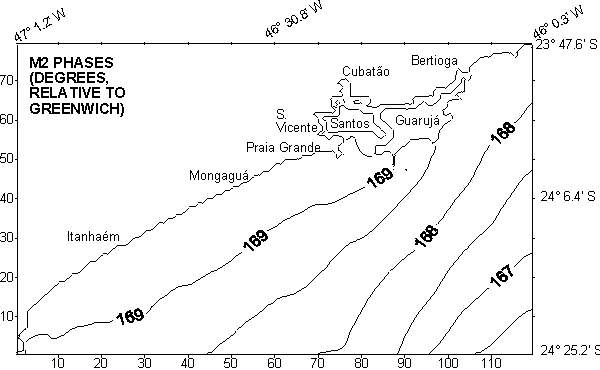
Fig. 2. M2 phases (relative to Greenwich) in Santos.
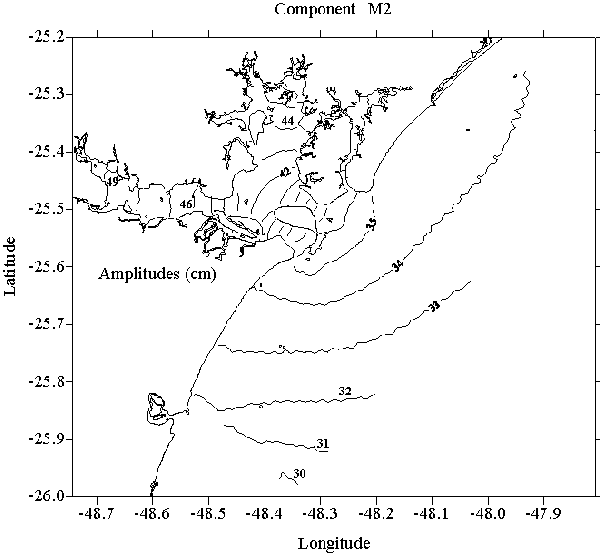
Fig. 3. M2 amplitudes in Paranaguá
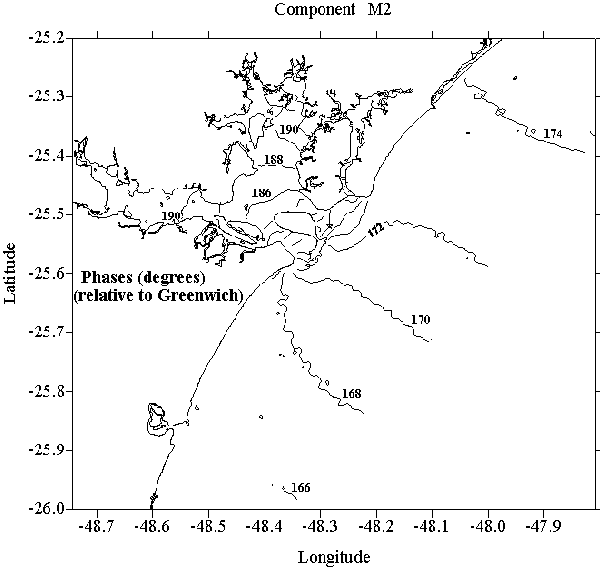
Fig. 4. M2 phases (relative to Greenwich) in Paranaguá.
The implemented models proved to be useful for both studies of characteristics of the tidal propagation and operational predictions of tides and tidal currents. Future improvements in the models should consider an increase of resolution, to a grid spacing of about 100 m, and the inclusion of meteorological effects and variations of density, in addition to the tides.
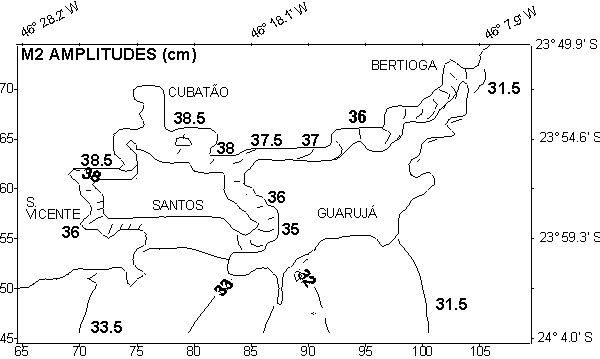
Fig. 5. M2 amplitudes in the shallow area of Santos.
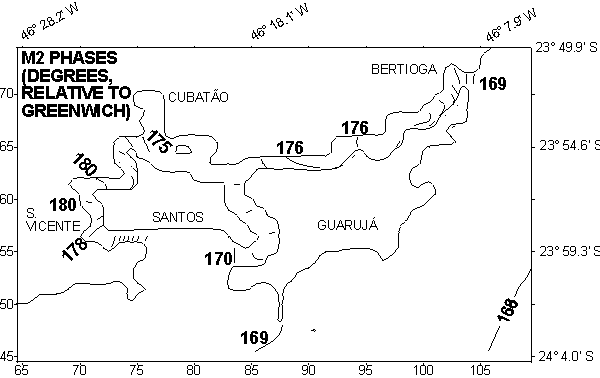
Fig. 6. M2 phases in the shallow area of Santos.
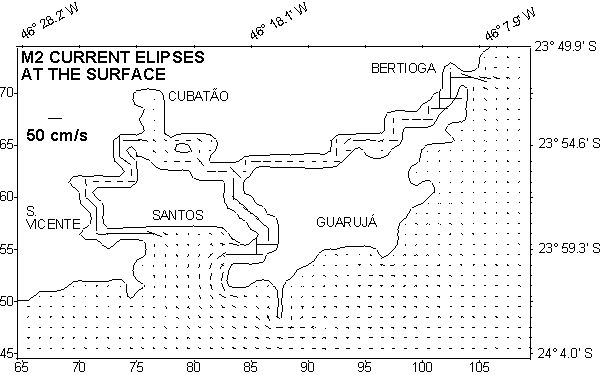
Fig. 7. M2 current ellipses at the surface, in the shallow area of
Santos
Acknowledgments
The authors wish to thank Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundacão de Amparo a Pesquisa do Estado de São Paulo (FAPESP), for their finantial support.
References
Blumberg, A. F. & Mellor, G. L. 1987. A description of a three-dimensional coastal ocean circulation model. In: Three-Dimensional Coastal Ocean Models, vol 4, Ed: N. S. Heaps, American Geophysical Union, Washington, D. C., USA, p. 1-16.
Franco, A. S. 1988. Tides - fundamentals, analysis and prediction. Public. FCTH Fundação Centro Tecnológico de Hidráulica, Escola Politécnica da USP, 2a Edição - 249 p.
Franco, A. S. & Harari, J. 1987. Computer programs for tidal data checking, correction, analysis and prediction by the harmonic method. Relat. int. Inst. oceanogr. Univ. S Paulo, 16:1-65.
Harari, J. & Camargo, R. 1994. Simulação da propagação das nove principais componentes de maré na plataforma sudeste brasileira através de modelo numérico hidrodinâmico. Bolm Inst. oceanogr., S Paulo, 42 (1):35-54.
Harari, J. & Camargo, R. 1997. "Simulações da circulação de maré na região costeira de Santos (SP) com modelo numérico hidrodinâmico". Pesquisa Naval - Suplemento Especial da Revista Marítima Brasileira, n° 10, p. 173 - 188.
HarariI, J. & Camargo, R. 1998. Modelagem numérica da região costeira de Santos (SP): circulação de maré. Rev. bras. oceanogr., S Paulo, 46(2):135-156.
Mellor, G. L. 1993. User's Guide for a three-dimensional, primitive equation, numerical ocean model. Princeton University, Internal Report, 35 p.
Oey, L. Y.; Mellor, G. L. & Hires, R. I. 1985. A three-dimensional
simulation of the Hudson - Raritan Estuary. Part I: Description of the
model and model simulations. Journal of Physical Oceanography, vol. 15,
p. 1676-1692.